منشأ اعداد اعشاری ۱۵۰ سال قدیمیتر از تصورات پیشین
به گزارش خبرگزاری علم و فناوری آنا به نقل از مجلۀ اسمیتسونین، مورخان برای سالها تصور میکردند که نقطۀ اعشار زمانی به وجود آمد که ریاضیدان آلمانی، کریستوفر کلاویئوس (Christopher Clavius) در سال 1593 از آن برای نوشتن محتوای ستارهشناسی استفاده کرد.
با این حال، شواهدی تازه یافتشده که نشان میدهد نقطۀ اعشار شاید 150 سال قدیمیتر از چیزی باشد که فکر میکردیم: بر اساس مقالهای که ماه گذشته در مجلۀ تاریخ ریاضیات (Historia Mathematica) منتشر شده است، گویا تاجری ونیزی از سدۀ پانزدهم به نام جوانی بیانکینی (Giovanni Bianchini) از این نشانۀ ریاضیاتی در اسنادی استفاده کرده که به سالهای 1441 تا 1450 برمیگردد.
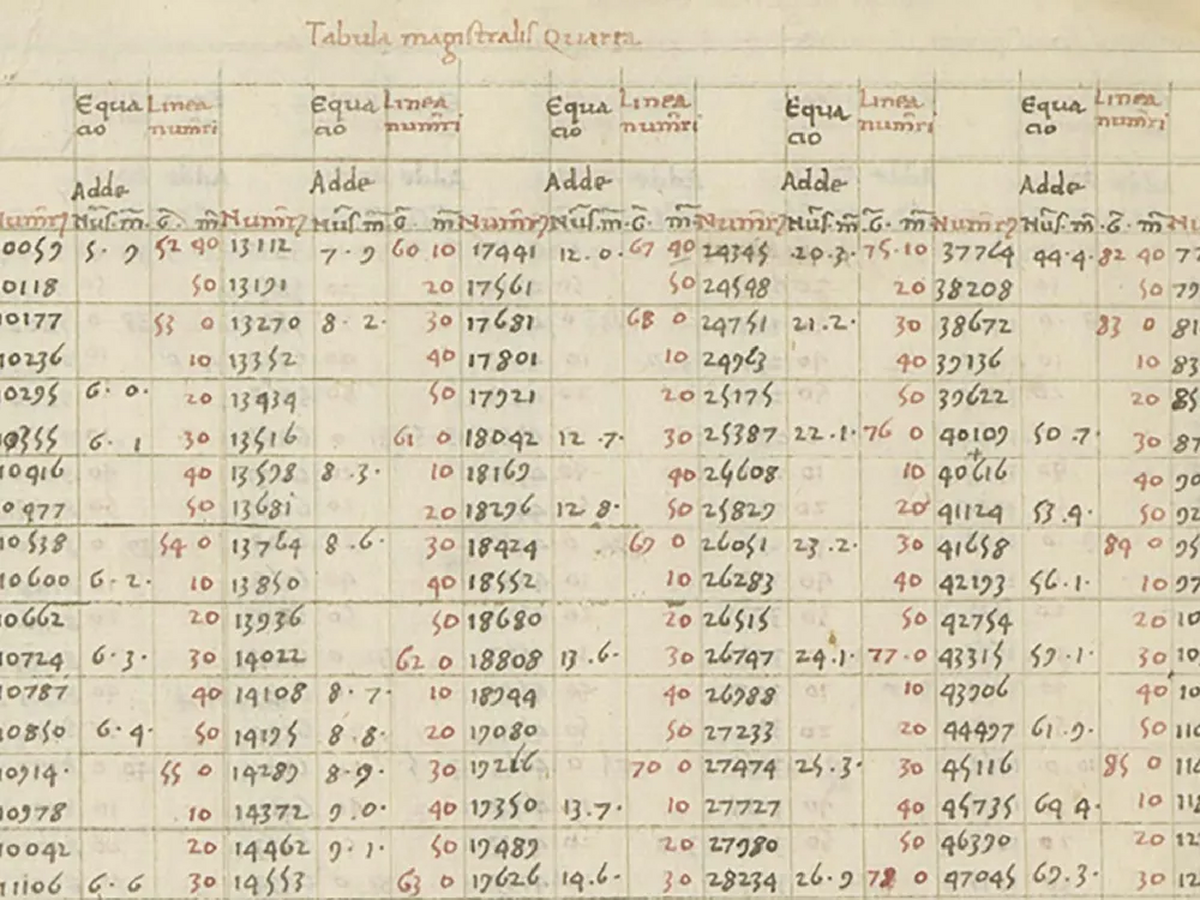
گلن فان بروملن (Glen Van Brummelen) نویسندۀ این پژوهش در دانشگاه ترینیتی کانادا (Trinity Western University) در پژوهشی راجع به تاریخ ریاضیات مشارکت دارد و هنگام آمادهشدن برای کلاس درس ریاضیات دبیرستان ناگهان متوجه چیزی عجیب میشود: روی یکی از دستنوشتههای لاتین بیانکینی عدد 10.4 نوشته شده بود و توضیح داده شده بود که چگونه باید 10.4 را در 8 ضرب کرد.
فان بروملن در مصاحبهای با مجلۀ نیچر توضیح میدهد: «متوجه شدم که دقیقاً مثل ما از اعداد اعشار استفاده میکند و در ضمن میداند چطور از آن در محاسبات استفاده کند. یادم میآید در حالی که کامپیوتر در دست داشتم، راهرو را بالا و پایین دویدم تا کسی را پیدا کنم که بیدار باشد و فریاد بزنم: «اینجا را نگاه! این یارو در دهۀ 1440 از اعشار استفاده کرده!»
جدولی که بروملن مطالعه میکرد، سندی است که توضیح میدهد چگونه مختصات سیارات محاسبه میشوند. در آن زمان، بیانکینی برای خانوادۀ استس (d’Estes) کار میکرد که خانوادۀ حاکم بر ونیز بودند. او که پیشتر تاجر بود و اکنون وزیر خانوادۀ استس شده بود، به این خانواده در تنظیم امور تجاری خود کمک میکرد، اما همزمان مسئول طراحی تقویمها نیز بود و بدین ترتیب وظیفه داشت از دانش خود دربارۀ مثلثات استفاده و آسمان شب را مطالعه کند. ستارهشناسان سدههای میانی طبیعتاً کامپیوتری نداشتند و برای محاسبات خود بر جدولهایی مشابه این متکی بودند.
فان بروملن توضیح میدهد: «تصور کنید از چنین جدولی استفاده میکنید: جدول به شما میگوید سینوس 43 درجه چقدر است. میگوید سینوس 44 درجه چقدر است. ولی سیارهها که ناگهان از یک درجه به درجۀ دیگر نمیپرند. سیارهها در خطی ممتد از بین این دو حرکت میکنند. پس شرایطی خواهد بود که مجبور شوید سینوس عددی بین 43 و 44 را محاسبه کنید. اینجاست که در این جدول با اعشار روبرو میشویم.»
این اکتشاف نشان میدهد که در سدههای میانه، بر خلاف باور عمومی، فعالیتهای علمی بسیاری در جریان بود و بشریت در رکود فکری فرو نرفته بود.
با این همه، نقطۀ اعشاری بیانکینی به ناگاه پذیرفته نشد. کلاویئوس پس از گذشت 150 سال، احتمالاً با مطالعۀ آثار بیانکینی با این علامت آشنا شد و از آن استفاده کرد.
پیش از این پژوهشگران متعجب بودند که چرا کلاویئوس به شکل محدود از اعشار استفاده کرده است و در آثار متاخر خود از آن بهره نمیبرد. به گفتۀ بروملن «چرا باید کسی سیستم تازه و قدرتمندی ابداع کند و از آن در زمینههای محدودی بهره ببرد و به ناگاه آن را کنار بگذارد؟» اما اگر کلاویئوس این سیستم را از جای دیگری گرفته باشد و کار کس دیگری را تکرار کرده باشد، رفتارش معنادار میشود.
با این که برخی از «انواع اعشار» بسیار قدیمیتر از «نقطۀ اعشار» هستند، تا زمان بیانکینی و کلاویئوس شاهد ظهور یک سیستم منسجم نبودهایم. پیش از این زمان، ریاضیدانان بیش از هر چیز بر کسر و ترکیبهای پیچیدۀ دیگر متکی بودند. وقتی همگان نقطۀ اعشار را پذیرفتند، محاسبات پیچیده در بسیاری از مواقع ساده شد.
به گفتۀ بوملن: «در واقع این نشان از قدرت سیستم اعداد اعشاری ماست، اینکه میتوانیم از یک سیستم شمارش برای حسابرسی به دفاتر، اندازهگیری مسافت، یا تبدیل اعداد در هر زمینهای استفاده کنیم. این سیستم شمارش جهانشمول است و نشان میدهد که ریاضیات از به همۀ وجوه زندگی انسان و تجربۀ انسان مرتبط است.»
انتهای پیام/